About Me
Junyang Lin (Justin)
Researcher in DAMO Academy, Alibaba Group
Google Scholar
Github
Intro:
I am Junyang (Justin) Lin, a researcher and engineer in the M6 team, Data Analytics and Intelligence Lab, DAMO Academy, Alibaba Group. I have been working on deep learning for NLP and multimodal representation learning. My research focuses are large-scale pretraining and its downstream application. In 2021, I led the project M6 (MultiModality-to-MultiModality Multitask Mega-transformer), which refers to the Chinese Multimodal Pretrainer, and developed the largest pretrained model M6-10T with my teammates. We also developed a large-scale platform of M6 for finetuning and inference, which supports a great numbers of applications and services in Alibaba Group, including AI designer, automatic text generation, cross-modal retrieval, visual grounding, natural language understanding, etc. In 2022, my team proposes OFA, a unified multimodal multitask pretrainer that achieved a series of SOTAs on benchmark datasets, say MSCOCO Image Captioning, VQA, RefCOCO (-/+/g), and I have been in charge of its opensourcing (OFA) on Github. In the near future, I plan to build an OFA system towards a real unified model for multitasking and multimodality.
Before graduation, I had been a member of Language Computing and Machine Learning Group (LANCO), Key Laboratory of Computational Linguistics, supervised by Xu Sun and Qi Su. My research interests are in natural language generation and graph computing. Specifically, I am now focusing on title generation, description generation and knowledge graph.
Research Interests:
NLP, Multi-modality, CV. Notably I focus on large-scale pretraining.
Academics

Selected Papers:
Junyang Lin, Rui Men, An Yang, Chang Zhou, Ming Ding, Yichang Zhang, Peng Wang, Ang Wang, Le Jiang, Xianyan Jia, Jie Zhang, Jianwei Zhang, Xu Zou, Zhikang Li, Xiaodong Deng, Jie Liu, Jinbao Xue, Huiling Zhou, Jianxin Ma, Jin Yu, Yong Li, Wei Lin, Jingren Zhou, Jie Tang, Hongxia Yang. M6: A Chinese Multimodal Pretrainer. arXiv 2021 (Note that this is an extension of my KDD paper "M6: Multi-Modality-to-Multi-Modality Multitask Mega-transformer for Unified Pretraining") [Paper]
Peng Wang, An Yang, Rui Men, Junyang Lin, Shuai Bai, Zhikang Li, Jianxin Ma, Chang Zhou, Jingren Zhou, Hongxia Yang. Unifying Architectures, Tasks, and Modalities Through a Simple Sequence-to-Sequence Learning Framework. arXiv 2022. [Paper] [Code]
Zixuan Ma, Jiaao He, Jiezhong Qiu, Huanqi Cao, Yuanwei Wang, Zhenbo Sun, Liyan Zheng, Haojie Wang, Shizhi Tang, Tianyu Zheng, Junyang Lin, Guanyu Feng, Zeqiang Huang, Jie Gao, Aohan Zeng, Jianwei Zhang, Runxin Zhong, Tianhui Shi, Sha Liu, Weimin Zheng, Jie Tang, Hongxia Yang, Xin Liu, Jidong Zhai, Wenguang Chen. BaGuaLu: targeting brain scale pretrained models with over 37 million cores. PPoPP 2022. [Paper]
Yu Huang, Junyang Lin, Chang Zhou, Hongxia Yang, Longbo Huang. Modality Competition: What Makes Joint Training of Multi-modal Network Fail in Deep Learning? (Provably). arXiv 2022. [Paper]
Junyang Lin, An Yang, Jinze Bai, Chang Zhou, Le Jiang, Xianyan Jia, Ang Wang, Jie Zhang, Yong Li, Wei Lin, Jingren Zhou, Hongxia Yang. M6-10T: A Sharing-Delinking Paradigm for Efficient Multi-Trillion Parameter Pretraining. [Paper]
Ming Ding, Zhuoyi Yang, Wenyi Hong, Wendi Zheng, Chang Zhou, Da Yin, Junyang Lin, Xu Zou, Zhou Shao, Hongxia Yang, Jie Tang. CogView: Mastering Text-to-Image Generation via Transformers. NeurIPS 2021 [Paper] [Code]
Shuhuai Ren, Junyang Lin, Guangxiang Zhao, Rui Men, An Yang, Jingren Zhou, Xu Sun, Hongxia Yang. Learning Relation Alignment for Calibrated Cross-modal Retrieval. ACL 2021. [Paper] [Code]
An Yang, Junyang Lin, Rui Men, Chang Zhou, Le Jiang, Xianyan Jia, Ang Wang, Jie Zhang, Jiamang Wang, Yong Li, Di Zhang, Wei Lin, Lin Qu, Jingren Zhou, Hongxia Yang. M6-T: Exploring Sparse Expert Models and Beyond. arXiv 2021. [Paper]
Peng Wang, Junyang Lin, An Yang, Chang Zhou, Yichang Zhang, Jingren Zhou, Hongxia Yang. Sketch and Refine: Towards Faithful and Informative Table-to-Text Generation. ACL 2021. [Paper]
Jingjing Xu, Liang Zhao, Junyang Lin, Rundong Gao, Xu Sun, Hongxia Yang. KNAS: Green Neural Architecture Search. ICML 2021. [Paper] [Code]
Junyang Lin, Rui Men, An Yang, Chang Zhou, Yichang Zhang, Peng Wang, Jingren Zhou, Jie Tang, Hongxia Yang. M6: Multi-Modality-to-Multi-Modality Multitask Mega-transformer for Unified Pretraining. KDD 2021. [Paper]
Junyang Lin, An Yang, Yichang Zhang, Jie Liu, Jingren Zhou, Hongxia Yang. InterBERT: Vision-and-Language Interaction for Multi-modal Pretraining. arXiv 2020. [Paper]
Qibin Chen, Junyang Lin, Yichang Zhang, Ming Ding, Yukuo Cen, Hongxia Yang, Jie Tang. Towards Knowledge-Based Recommender Dialog System. EMNLP 2019. [Paper] [Code]
Jingjing Xu, Xu Sun, Zhiyuan Zhang, Guangxiang Zhao, Junyang Lin. Understanding and Improving Layer Normalization. NeurIPS 2019. [Paper] [Code]
Qibin Chen, Junyang Lin, Yichang Zhang, Hongxia Yang, Jingren Zhou, Jie Tang. Towards Knowledge-Based Personalized Product Description Generation in E-commerce. KDD 2019. [Paper] [Code]
Bingzhen Wei, Mingxuan Wang, Hao Zhou, Junyang Lin, Xu Sun. Imitation Learning for Non-Autoregressive Neural Machine Translation. ACL 2019. [Paper]
Guangxiang Zhao, Junyang Lin, Zhiyuan Zhang, Xuancheng Ren, Qi Su, Xu Sun. Explicit Sparse Transformer: Concentrated Attention Through Explicit Selection. arXiv 2019. [Paper] [Code]
Junyang Lin, Xu Sun, Shuming Ma, Qi Su. Global Encoding for Abstractive Summarization. ACL 2018. [Paper] [Code]
Junyang Lin, Qi Su, Pengcheng Yang, Shuming Ma, Xu Sun. Semantic-Unit-Based Dilated Convolution for Multi-Label Text Classification. EMNLP 2018. [Paper] [Code]
Jingjing Xu, Xuancheng Ren, Junyang Lin, Xu Sun. Diversity-Promoting GAN: A Cross-Entropy Based Generative Adversarial Network for Diversified Text Generation. EMNLP 2018. [Paper] [Code]
Academic Activities:
Reviewer of ICML, NeurIPS, ACL, etc.
Blog

Introduction to Deep Learning (PPT).
Another Perspective to View SVM (1)

This is what I can never forget. Nine months ago, my mentor said to me:"Hey, how about building a paraphrasing system for your final project? Well try to do some feature engineering, label your data, and use SVM?" Ooh, maan, I can only write no more than ten lines of code at that time and you told me to build a system with a Support Vector Machine?! Is it a machine that I can afford? Er mar gerd... Back to our topic, since then, I have had a special feeling for SVM and I have always been curious about such black magic. In the following content, I am going to focus on the loss function of SVM and it involves some knowledge about square error and cross entropy.
Support Vector Machine has nothing to do with a real machine. It is just a great machine learning algorithm which often has excellent performance in binary classification. Training a SVM model helps us find the best hyperplane (just like a plane in the high dimensional space) to separate the data and classify them to the right categories. Its main difference from perceptron is that it not only separates the data but also maximizes the margin. Here I do not want to discuss about details about functional margin and geometric margin. I try to illustrate it in a more intuitive way. Say, you have a bunch of data, like ten thousand documents with five thousand of positive attitude and another five thousand of negative attitude, and you want to train a model that can classify them. The procedure is relatively simple: you just need to turn the documents into feature vectors with labels, $+1$ for positive and $-1$ for negative. Suppose the data are linear separable, there should be a hyperplane that can best separate them with largest margin. Intuitively, on either side, there should be some vectors that are nearest to the hyperplane, which are support vectors. These vectors are on two hyperplanes that are parallel to the best hyperplane, $H_1$ and $H_2$, and the distance between $H_1$ and $H_2$ is margin. This is not difficult, but the problem is, how can we find such hyperplane? If you find some books to read, you will see a lot about convex quadratic programming using Lagrange function, which is really puzzling. However, I learned a lot from Hung-yi Lee, a professor in NTU, that training SVM can be viewed from another perspective, which I think is much simpler. If you know something about Pegasos, the fact that SVM can be trained with gradient descent may seem obvious to you. In the following parts, I am going to discuss about this issue.
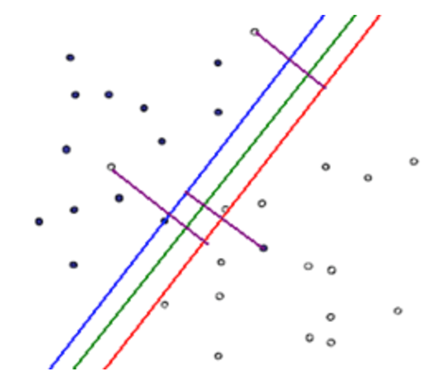
Let's define the functions for linear separable SVM first. We have a bunch of feature vectors \(\mathcal{X} = \{x^{(1)}, x^{(2)}, ..., x^{(n)}\}\), corresponding to the label space \(\mathcal{Y} = \{+1, -1\}\), and now we use an affine function \(f(x) = w^{T}x + b\) to model the data points, and our task is to find the best hyperplane \(w^{*T}x + b^{*} = 0\) to separate them. For a certain data point $x^{(i)}$, if it is correctly classified, \(y^{(i)}f(x^{(i)}) > 0\). This is simple, but adding margin maximization problem to it makes it much more complicated. Instead of discussing about the functional and geometrical margin as well as convex quadratic programming, I would like to talk about the choice of loss function for a linear classifier.
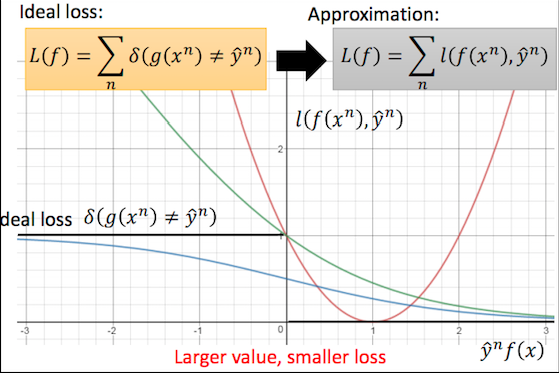
(From Hung-yi Lee's PPT in the Lecture 20 of Machine Learning)
As is shown in the picture, the x axis represents $y^{(n)}f(x^{(n)})$, while the y axis represents the loss. In fact we have an ideal loss, which is \(l(g(x^{(n)}), y^{(n)}) = \delta(g(x^{(n)}) \neq y^{(n)})\), where \(g(x^{(n)}) = sign(f(x^{(n)}))\). However, it is problematic in application since it is totally not differentiable. Therefore, we need to find some alternatives, including L2 loss, sigmoid square loss, cross entropy loss and hinge loss. First of all, it is impossible to train a linear classifier with L2 loss function (\(l(f(x^{(n)}), y^{(n)}) = (y^{(n)}f(x^{(n)})-1)^2\), see the red curve). We hope that the target $y^{(n)}$ and the output $f(x^{(n)})$ are of the same sign, and we also hope that the larger their product is, the smaller the loss is, so using mean square error here is definitely inapproapriate. Second of all, sigmoid square loss is also not a good choice (\(l(f(x^{(n)}), y^{(n)}) = (\sigma(y^{(n)}f(x^{(n)}))-1)^2\)). If you have ever experienced the problem of vanishing gradient in your training of neural network, you can find that the problem here is similar. If the value $y^{(n)}f(x^{(n)})$ is a large negative number, its derivative is close to $0$, which means the gradient is too small for the loss to move downward. So how about cross entropy loss? I think it is a reasonable choice and its performance may be satisfactory. The loss function is \(l(f(x^{(n)}), y^{(n)}) = log(1 + exp(-y^{(n)}f(x^{(n)}))\). It seems great since it is the upper bound of the ideal loss and it is consistent with the rule "the larger value, the smaller loss". Moreover, when the $y^{(n)}f(x^{(n)})$ is negative, it has large gradient, which encourages the loss to move downward. However, is there even a better loss function? We may find that the problem of this function is that it encourages the value to be as large as possible, but in fact, if the value is larger than a certain number, our requirements are all satisfied and there is no need for it to be even larger. It may be not robust enough and may be influenced by the outliers.
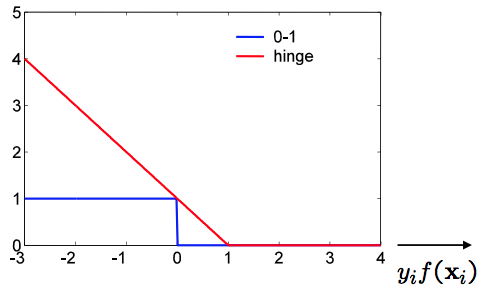
(From Andrew Zisserman's PPT in the Lecture 2 of Machine Learning)
This function is pretty simple: $$l(f(x^{(n)}), y^{(n)}) = max(0, 1 - y^{(n)}f(x^{(n)}))$$ It means that when the value is negative, the loss is large and it encourages the value to become positive. Moreover, being positive is not enough and it should be larger than a certain value, here we set the value $1$. When the value is larger than 1, there is no need to decrease the loss because we now have enough confidence that we have correctly classified the data points, which solves the problem mentioned above. The value $1$ is actually our margin. You can try to prove it from the perspective of functional margin and geometrical margin. Now there is a problem about the value of the margin. The reason why it should be $1$ is that it makes the loss function a tight, or in another word, lowest upper bound of the ideal loss.
Now that the problem becomes clear, we can build the final loss function for linear SVM: $$L(f) = \sum_{i=1}^{n}l(f(x^{(i)}), y^{(i)}) + \frac{\lambda}{2}||w||_2^2$$ Well, is it similar to the optimization problem that you are familiar with? $$min\frac{1}{2}||w||_2^2 + C\sum_{i=1}^{n}\xi^{(i)}$$ $$subject \; to \; y^{(i)}f(x^{(i)}) \geq 1 - \xi^{(i)}$$ Here the $\xi^{(i)}$ is our slack variable, which is also our hinge loss function. Wow, it is just like magic!
I have to admit that the first time I learned these ideas I jumped off my chair excitedly. Even today I still feel that this perspective is really great for beginners to understand linear SVM. I hope I can share the happiness to you guys. Next time I will try to discuss about kernel tricks in SVM, starting from gradient descent of SVM.
Another Perspective to View SVM (2)
In this part, I am going to prove that $w$ is the linear combination of the inputs $x$. In the last passage, I discussed about the loss function of SVM and showed that it can be trained with gradient descent. Here I would like to present the training steps by calculating the gradients.
The hinge loss function of SVM is: $$l(f(x^{(n)}), \hat{y}^{(n)})=max(0, 1 - \hat{y}^{(n)}f(x^{(n)}))$$ The derivative of $l(f(x^{(n)}), \hat{y}^{(n)})$ to $w_i$ can be calculated below: $$\frac{\partial{l}}{\partial{w_i}}=\frac{\partial{l}}{\partial{f}}\frac{\partial{f}}{\partial{w_i}}=\begin{cases} -\hat{y}^{(n)}x^{(n)}_i& 1-\hat{y}^{(n)}f(x^{(n)}) > 0 \\ 0& 1-\hat{y}^{(n)}f(x^{(n)}) \le 0 \end{cases}$$ so the gradient of $w_i$ is: $$\nabla{w_i}=\frac{\partial{L}}{\partial{w_i}}=\sum_{n}-\delta(\hat{y}^{(n)}f(x^{(n)})<1)\hat{y}^{(n)}x^{(n)}_{i}$$ and the gradient of the weight vector is: $$\nabla{w}=\frac{\partial{L}}{\partial{w}}=\sum_{n}-\delta(\hat{y}^{(n)}f(x^{(n)})<1)\hat{y}^{(n)}x^{(n)}$$ In the optimization procedure, the weight vector $w$ is optimized in each step in the following way: $$w=w-\eta\nabla{w}$$ If the weight vector reaches its global minimum in $m$ steps, which means the optimal $w^{*}$ is obtained, \nabla{w}=0. Therefore, if $w$ is initialized as $0$, $w^{*}$ can be presented as follows: $$w^{*}=m\cdot(-\eta\nabla{w})=\sum_{n}m\eta\delta(\hat{y}^{(n)}f(x^{(n)})<1)\hat{y}^{(n)}x^{(n)}$$ Now I define a term called $\alpha_{n}$, that: $$\alpha_{n}=m\eta\delta(\hat{y}^{(n)}f(x^{(n)})<1)$$ Then $w^{*}$ can be written as below: $$w^{*}=\sum_{n}\alpha_{n}\hat{y}^{(n)}x^{(n)}$$ This equation is the same of $w^{*}$ in the Lagrange function for solving the dual problem of SVM, and it proves that $w$ is a linear combination of the data points $x$. Here the equation can be further simplified to: $$w=\sum_{n}\alpha_{n}^{*}x^{(n)}=X\alpha^{*}$$ It should be noted that because of $\delta$ in $\alpha^{*}$, the vector $\alpha^{*}$ is sparse. The vectors $x^{(n)}$ with non-zero $\alpha_{n}^{*}$ are the support vectors holding the margin.
Back to the affine function $f(x)=w^{T}x$, now it can be changed to: $$f(x)=\alpha^{T}X^{T}x=\sum_{n}\alpha_{n}(x_{n}\cdot{x})$$ Here I define a function called K that: $$K(x_{n}, x)=\sum_{n}x_{n}\cdot{x}$$ so: $$f(x)=\sum_{n}\alpha_{n}K(x_{n}\cdot{x})$$ Function K is called kernel function (here this K function is linear kernel function), which projects the input data from the input space to the feature space, usually of higher dimensions. The calculation of $K(x, z)$ is much simpler than projection function $\phi(x)$. Moreover, the power of kernel function is more than simple calculation. It is able to project the inputs from the inputs space to the space of infinite dimensions. One typical example is the well-known RBF function.
In the next passage, I am going to introduce the traditional method to solve the primal problem of SVM, and try my best to interpret Lagrange multiplier, which has puzzled me for a long time, compared with L2 regularization.
Intro to Deep Learning (PPT)
The following link is my PPT for a lecture in the course Computational Linguistics at our institute, which is a simple introduction to deep learning. If you are interested, please click here!
Résumé

To read my résumé, please click here!
Contact

Email: junyang.ljy@alibaba-inc.com
Address: Jinhui Building, Chaoyang District, Beijing, China
Elements
Text
This is bold and this is strong. This is italic and this is emphasized.
This is superscript text and this is subscript text.
This is underlined and this is code: for (;;) { ... }. Finally, this is a link.
Heading Level 2
Heading Level 3
Heading Level 4
Heading Level 5
Heading Level 6
Blockquote
a a
Preformatted
i = 0;
while (!deck.isInOrder()) {
print 'Iteration ' + i;
deck.shuffle();
i++;
}
print 'It took ' + i + ' iterations to sort the deck.';
Lists
Unordered
- Dolor pulvinar etiam.
- Sagittis adipiscing.
- Felis enim feugiat.
Alternate
- Dolor pulvinar etiam.
- Sagittis adipiscing.
- Felis enim feugiat.
Ordered
- Dolor pulvinar etiam.
- Etiam vel felis viverra.
- Felis enim feugiat.
- Dolor pulvinar etiam.
- Etiam vel felis lorem.
- Felis enim et feugiat.
Icons
Actions
Table
Default
| Name |
Description |
Price |
| Item One |
Ante turpis integer aliquet porttitor. |
29.99 |
| Item Two |
Vis ac commodo adipiscing arcu aliquet. |
19.99 |
| Item Three |
Morbi faucibus arcu accumsan lorem. |
29.99 |
| Item Four |
Vitae integer tempus condimentum. |
19.99 |
| Item Five |
Ante turpis integer aliquet porttitor. |
29.99 |
|
100.00 |
Alternate
| Name |
Description |
Price |
| Item One |
Ante turpis integer aliquet porttitor. |
29.99 |
| Item Two |
Vis ac commodo adipiscing arcu aliquet. |
19.99 |
| Item Three |
Morbi faucibus arcu accumsan lorem. |
29.99 |
| Item Four |
Vitae integer tempus condimentum. |
19.99 |
| Item Five |
Ante turpis integer aliquet porttitor. |
29.99 |
|
100.00 |



